Tools Required
J 38792-A Electronic Vibration Analyzer (EVA) 2
Tire and Wheel Rotational Speed Calculation
A size P235/75R15 tire rotates ONE complete revolution per second (RPS), or 1 Hz, at a vehicle speed of 8 km/h (5 mph). This means that at 16 km/h (10 mph), the same tire will make TWO complete revolutions in one second, 2 Hz, and so on.
Tire Size | Tread | Revs/Sec (Hertz) at 8 km/h (5 mph) |
|---|---|---|
P225/60R16 | ALS | 1.08 |
P225/60R16 | AL2 | 1.08 |
P235/55R17 | ALS | 1.06 |
P245/50R18 | AL3 | 1.04 |
Tread Codes | ||
ALS | All Season | |
AL2 | All Season Touring | |
- Determine the rotational speed of the tires in revolutions per second (RPS), or Hertz (Hz), at 8 km/h (5 mph), based on the size of the tires. Refer to the preceding Tire Rotational Speed table.
- Determine the number of increments of 8 km/h (5 mph) that are present, based on the vehicle speed (km/h, mph) at which the disturbance occurs.
- Determine the rotational speed of the tires in revolutions per second (Hz), at the specific vehicle speed (km/h, mph) at which the disturbance occurs.
- Compare the rotational speed of the tires at the specific vehicle speed at which the disturbance occurs, to the dominant frequency recorded on the J 38792-A during testing. If the frequencies match, then a first-order disturbance related to the rotation of the tire/wheel assemblies is present.
- To compute higher order tire/wheel assembly rotation related disturbances, multiply the rotational speed of the tires at the specific vehicle speed at which the disturbance occurs, by the order number:
For example: According to the Tire Rotational Speed table, a P225/60R16 tire makes 1.08 revolutions per second (Hz) at a vehicle speed of 8 km/h (5 mph). This means that for every increment of 8 km/h (5 mph) in vehicle speed, the tire's rotation increases by 1.08 revolutions per second (Hz).
For example: Assume that a disturbance occurs at a vehicle speed of 96 km/h (60 mph). A speed of 96 km/h (60 mph) has 12 INCREMENTS of 8 km/h (5 mph):
96 km/h (60 mph) divided by 8 km/h (5 mph) = 12 increments
For example: To determine the tire rotational speed at 96 km/h (60 mph), multiply the number of increments of 8 km/h (5 mph) by the revolutions per second (Hz) for one increment:
12 increments X 1.08 Hz = 12.96 Hz, rounded to 13 Hz
If the frequencies do not match, then the disturbance may be related to a higher order of tire/wheel assembly rotation.
13 Hz X 2 , for second order = 26 Hz second-order tire/wheel assembly rotation related
13 Hz X 3 , for third order = 39 Hz third-order tire/wheel assembly rotation related
If any of these computations match the frequency of the disturbance, a disturbance of that particular order, relating to the rotation of the tire/wheel assemblies and/or driveline components (also rotating at the same speed) is present.
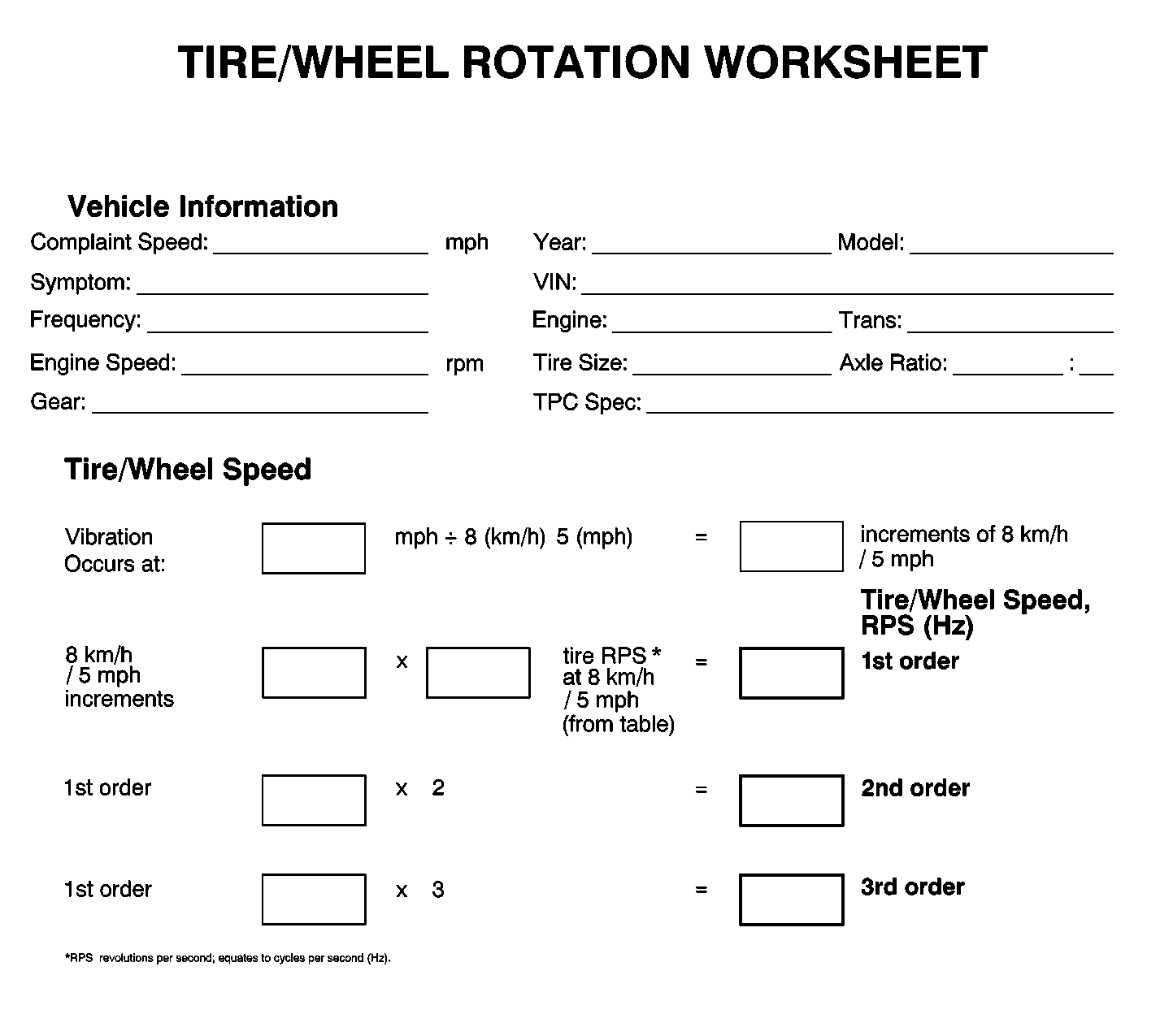
Component Rotational Speed Worksheet
Utilize the following worksheet as an aid in calculating the first, second and third order of tire/wheel assembly rotational speed related disturbances that may be present in the vehicle.
If after completing the Tire/Wheel Rotation Worksheet, the frequencies calculated do NOT match the dominant frequency of the disturbance recorded during testing, either recheck the data, or attempt to rematch the figures allowing for 1½-8 km/h (1-5 mph) of speedometer error.
If the possible tire/wheel assembly rotational speed related frequencies still do not match the dominant frequency of the disturbance, the disturbance is most likely torque/load sensitive.
If after completing the Tire/Wheel Rotation Worksheet, one of the frequencies calculated DOES match the dominant frequency of the disturbance, the disturbance is related to the rotation of that component group - tire/wheel assembly related.